Instrumental variables I
Materials for class on Monday, November 11, 2019
Contents
Slides
Download the slides from today’s class.

Running R from your computer
Download and unzip this folder to get started:
IV/2SLS examples
library(tidyverse) # For ggplot, %>%, and friends
library(broom) # For converting models to data frames
library(huxtable) # For side-by-side regression tables
library(AER) # For some econometrics datasets
library(wooldridge) # More econometrics datasets
library(estimatr) # For iv_robustEducation, wages, and parent education (fake data)
Download this data and put it in a folder named “data” in your project root:
We’re interested in the perennial econometrics question of whether an extra year of education causes increased wages. In this example we use simulated/fake data that includes the following variables:
| Variable name | Description |
|---|---|
wage |
Weekly wage |
educ |
Years of education |
ability |
Magical column that measures your ability to work and go to school (omitted variable) |
fathereduc |
Years of education for father |
If we could actually measure ability, we could estimate this model, which closes the confounding backdoor posed by ability and isolates just the effect of education on wages:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -80.2626923 | 5.6585424 | -14.18434 | 0 |
| educ | 9.2424696 | 0.3426683 | 26.97206 | 0 |
| ability | 0.2580724 | 0.0071809 | 35.93874 | 0 |
However, in real life we don’t have ability, so we’re stuck with a naive model:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -53.08545 | 8.4920070 | -6.251225 | 0 |
| educ | 12.24036 | 0.5033011 | 24.320144 | 0 |
The naive model overestimates the effect of education on wages (12.2 vs. 9.24) because of omitted variable bias. Education suffers from endogeneity—there are things in the model (like ability, hidden in the error term) that are correlated with it. Any estimate we calculate will be wrong and biased because of selection effects or omitted variable bias (all different names for endogeneity).
To fix the endogeneity problem, we can use an instrument to remove the endogeneity from education and instead use a special exogeneity-only version of education. Perhaps someone’s father’s education can be an instrument for education.
To be a valid instrument, it must meet three criteria:
- Relevance: Instrument is correlated with policy variable
- Exclusion: Instrument is correlated with outcome only through the policy variable
- Exogeneity: Instrument isn’t correlated with anything else in the model (i.e. omitted variables)
We can first test relevance by making a scatterplot and running a model of policy ~ instrument:
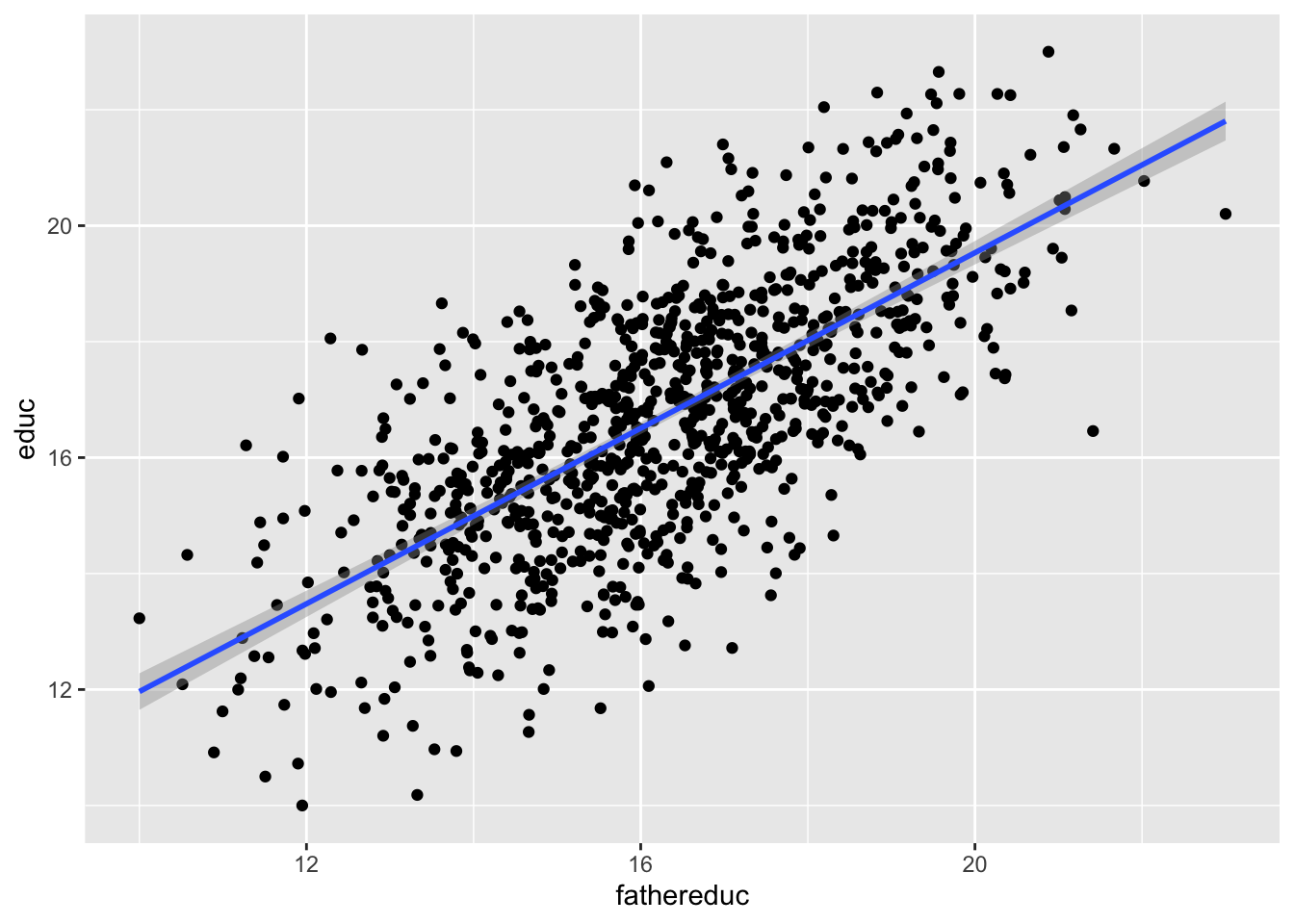
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 4.3955891 | 0.3986274 | 11.02681 | 0 |
| fathereduc | 0.7569158 | 0.0242786 | 31.17622 | 0 |
| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.4933898 | 0.4928822 | 1.595708 | 971.9564 | 0 | 2 | -1885.255 | 3776.51 | 3791.233 | 2541.192 | 998 |
This looks pretty good! The F-statistic is definitely above 10 (it’s 972!), and there’s a significant relationship between the instrument and policy. I’d say that this is relevant.
To check for exclusion, we need to see if there’s a relationship between father’s education and wages that occurs only because of education. If we plot it, we’ll see a relationship:
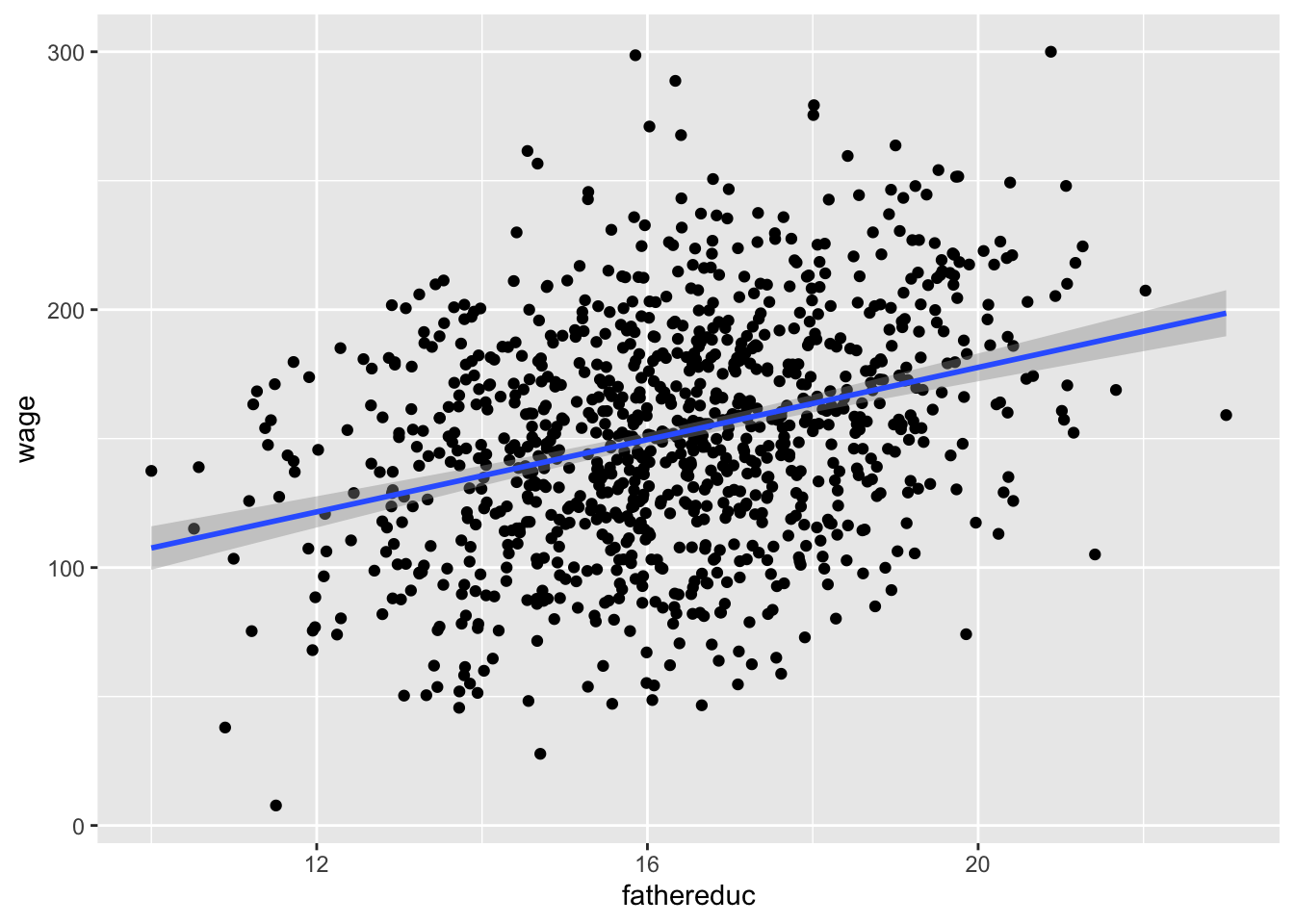
That’s to be expected, since in our model, father’s education causes education which causes wages—they should be correlated. We have to use theory to justify the idea that a father’s education increases the hourly wage only because it increases one’s education, and there’s no real statistical test for that.
There’s not really a test for exogeneity either, since there’s no way to measure other endogenous variables in the model (that’s the whole reason we’re using IVs in the first place!). Becuase we have the magical ability column in this fake data, we can test it. Father’s education shouldn’t be related to ability:
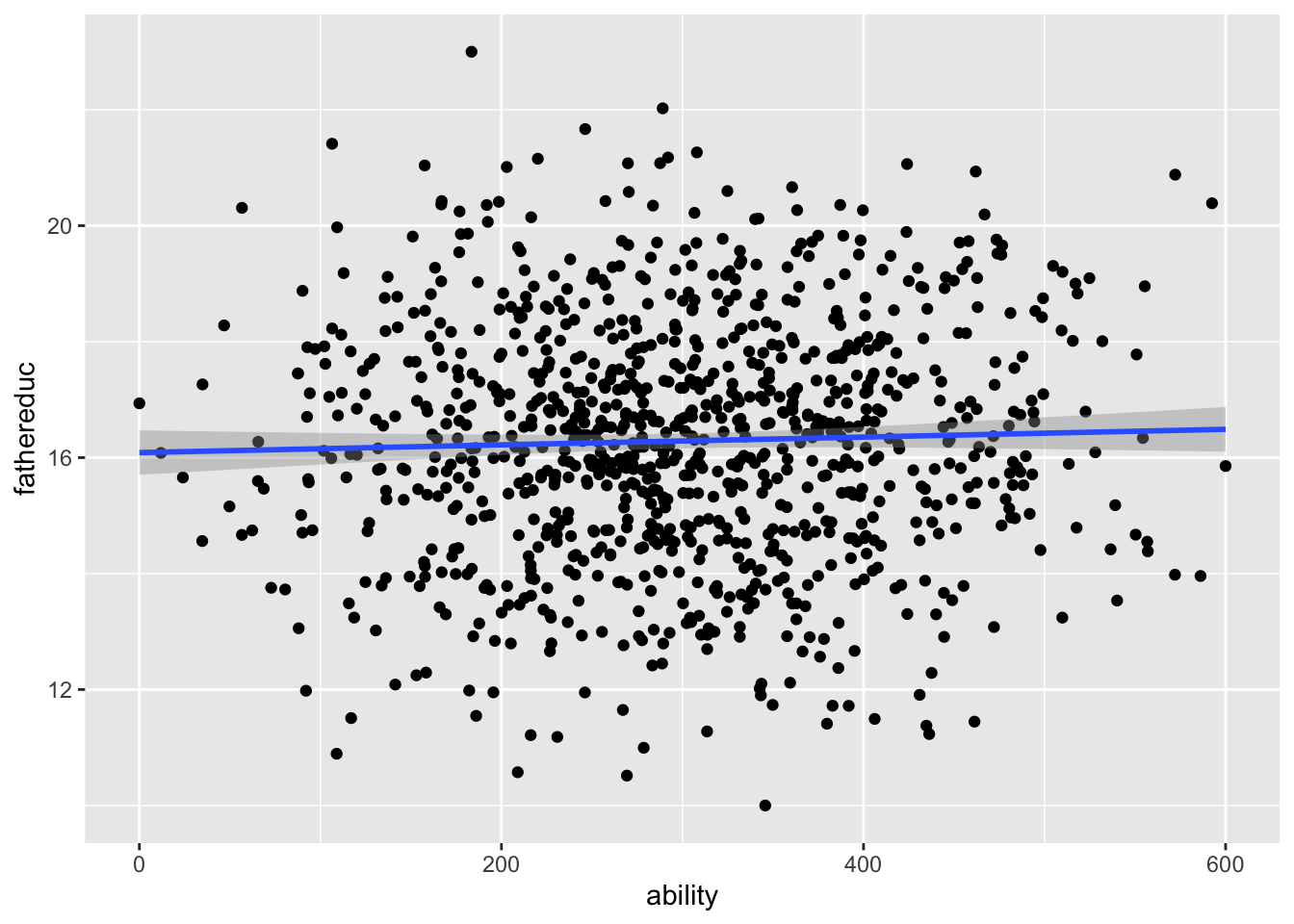
And it’s not! We can safely say that it meets the exclusion assumption.
For the last part—the exogeneity assumption—there’s no statistical test. We just have to tell a theory-based story that the number of years of education one’s father has is not correlated with anything else in the model (including any omitted variables). Good luck with that—it’s probably not a good instrument. This relates to Scott Cunningham’s argument that instruments have to be weird. According to Scott:
The reason I think this is because an instrument doesn’t belong in the structural error term and the structural error term is all the intuitive things that determine your outcome. So it must be weird, otherwise it’s probably in the error term.
Let’s just pretend that father’s education is a valid instrument and move on :)
Now we can do two-stage least squares (2SLS) regressin and use the instrument to filter out the endogenous part of education. The first stage predicts education based on the instrument (we already ran this model earlier when checking for relevance, but we’ll do it again just for fun):
Now we want to add a column of predicted education to our original dataset. The easiest way to do that is with the augment_columns() function from the broom library:
| wage | educ | ability | fathereduc | .fitted | .se.fit | .resid | .hat | .sigma | .cooksd | .std.resid |
|---|---|---|---|---|---|---|---|---|---|---|
| 146.3478 | 18.05319 | 348.2400 | 17.15832 | 17.38299 | 0.0547177 | 0.6701995 | 0.0011758 | 1.596367 | 0.0001040 | 0.4202485 |
| 147.5996 | 15.84549 | 181.1607 | 13.98853 | 14.98373 | 0.0752312 | 0.8617548 | 0.0022227 | 1.596274 | 0.0003256 | 0.5406466 |
| 161.8202 | 15.10521 | 337.3677 | 15.99431 | 16.50194 | 0.0509579 | -1.3967293 | 0.0010198 | 1.595895 | 0.0003915 | -0.8757505 |
| 105.0829 | 16.45813 | 106.4580 | 21.41317 | 20.60356 | 0.1343020 | -4.1454269 | 0.0070837 | 1.591062 | 0.0242457 | -2.6071108 |
| 167.5622 | 18.79382 | 301.5100 | 16.45763 | 16.85263 | 0.0506309 | 1.9411855 | 0.0010068 | 1.595323 | 0.0007464 | 1.2171170 |
| 172.9273 | 16.01597 | 283.6524 | 15.42531 | 16.07125 | 0.0546236 | -0.0552788 | 0.0011718 | 1.596507 | 0.0000007 | -0.0346625 |
Note a couple of these new columns. .fitted is the fitted/predicted value of education, and it’s the version of education with endogeneity arguably removed. .resid shows how far off the prediction is from educ. The other columns don’t matter so much.
Instead of dealing with weird names like .fitted, I like to rename the fitted variable to something more understandable after I use augment_columns:
ed_fake_with_prediction <- augment_columns(first_stage, ed_fake) %>%
rename(educ_hat = .fitted)
head(ed_fake_with_prediction)| wage | educ | ability | fathereduc | educ_hat | .se.fit | .resid | .hat | .sigma | .cooksd | .std.resid |
|---|---|---|---|---|---|---|---|---|---|---|
| 146.3478 | 18.05319 | 348.2400 | 17.15832 | 17.38299 | 0.0547177 | 0.6701995 | 0.0011758 | 1.596367 | 0.0001040 | 0.4202485 |
| 147.5996 | 15.84549 | 181.1607 | 13.98853 | 14.98373 | 0.0752312 | 0.8617548 | 0.0022227 | 1.596274 | 0.0003256 | 0.5406466 |
| 161.8202 | 15.10521 | 337.3677 | 15.99431 | 16.50194 | 0.0509579 | -1.3967293 | 0.0010198 | 1.595895 | 0.0003915 | -0.8757505 |
| 105.0829 | 16.45813 | 106.4580 | 21.41317 | 20.60356 | 0.1343020 | -4.1454269 | 0.0070837 | 1.591062 | 0.0242457 | -2.6071108 |
| 167.5622 | 18.79382 | 301.5100 | 16.45763 | 16.85263 | 0.0506309 | 1.9411855 | 0.0010068 | 1.595323 | 0.0007464 | 1.2171170 |
| 172.9273 | 16.01597 | 283.6524 | 15.42531 | 16.07125 | 0.0546236 | -0.0552788 | 0.0011718 | 1.596507 | 0.0000007 | -0.0346625 |
We can now use the new educ_hat variable in our second stage model:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -3.107953 | 14.3703343 | -0.2162757 | 0.8288171 |
| educ_hat | 9.251863 | 0.8555225 | 10.8142831 | 0.0000000 |
The estimate for educ_hat is arguably more accurate now because we’ve used the instrument to remove the endogenous part of education and should only have the exogenous part.
We can put all the models side-by-side to compare them:
| Perfect | OLS | 2SLS | |
| (Intercept) | -80.263 *** | -53.085 *** | -3.108 |
| (5.659) | (8.492) | (14.370) | |
| educ | 9.242 *** | 12.240 *** | |
| (0.343) | (0.503) | ||
| ability | 0.258 *** | ||
| (0.007) | |||
| educ_hat | 9.252 *** | ||
| (0.856) | |||
| N | 1000 | 1000 | 1000 |
| R2 | 0.726 | 0.372 | 0.105 |
| logLik | -4576.101 | -4991.572 | -5168.868 |
| AIC | 9160.202 | 9989.144 | 10343.735 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |||
Note how the coefficient for educ_hat in the 2SLS model is basically the same as the coefficient for educ in the perfect model that accounts for ability. That’s the magic of instrumental variables!
Education, wages, and parent education (real data)
This data comes from the wage2 dataset in the wooldridge R package (and it’s real!). Wages are measured in monthly earnings in 1980 dollars.
ed_real <- wage2 %>%
rename(education = educ, education_dad = feduc, education_mom = meduc) %>%
na.omit() # Get rid of rows with missing valuesWe want to again estimate the effect of education on wages, but this time we’ll use both one’s father’s education and one’s mother’s education as instruments. Here’s the naive estimation of the relationship, which suffers from endogeneity:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 175.15999 | 92.838561 | 1.886716 | 0.0596366 |
| education | 59.45181 | 6.697942 | 8.876131 | 0.0000000 |
This is wrong though! Education is endogenous to unmeasured things in the model (like ability, which lives in the error term). We can isolate the exogenous part of education with an instrument.
Before doing any 2SLS models, we want to check the validity of the instruments. Remember, for an instrument to be valid, it should meet these criteria:
- Relevance: Instrument is correlated with policy variable
- Exclusion: Instrument is correlated with outcome only through the policy variable
- Exogeneity: Instrument isn’t correlated with anything else in the model (i.e. omitted variables)
We can check for relevance by looking at the relationship between the instruments and education:
# Combine father's and mother's education into one column so we can plot both at the same time
ed_real_long <- ed_real %>%
pivot_longer(cols = c(education_dad, education_mom),
names_to = "instrument", values_to = "instrument_value")
ggplot(ed_real_long, aes(x = instrument_value, y = education)) +
geom_point() +
geom_smooth(method = "lm") +
facet_wrap(~ instrument)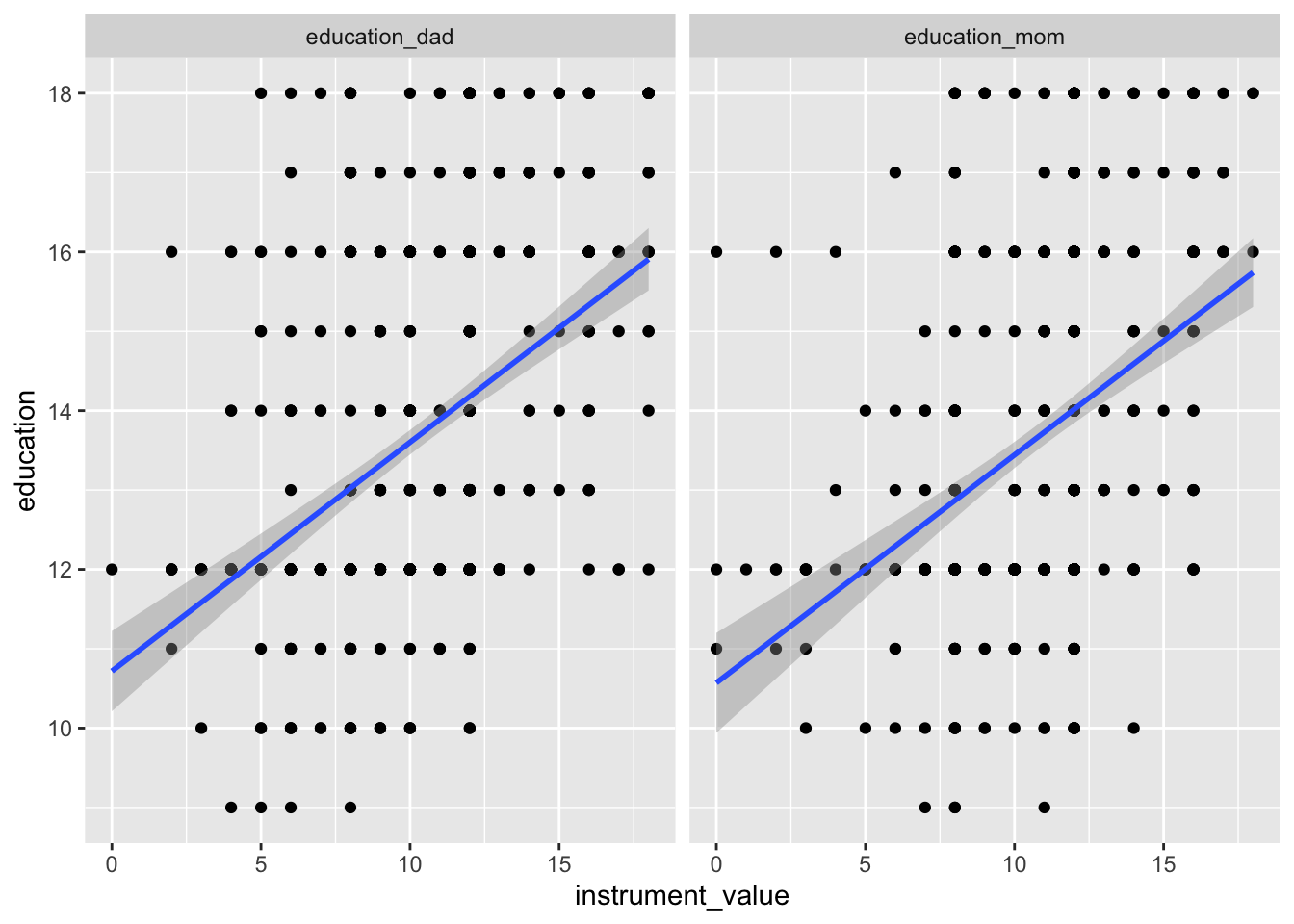
model_check_instruments <- lm(education ~ education_dad + education_mom,
data = ed_real)
tidy(model_check_instruments)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 9.9132852 | 0.3195911 | 31.018649 | 0.00e+00 |
| education_dad | 0.2189424 | 0.0288925 | 7.577836 | 0.00e+00 |
| education_mom | 0.1401693 | 0.0336511 | 4.165370 | 3.52e-05 |
| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.2015354 | 0.1991158 | 1.996932 | 83.29321 | 0 | 3 | -1397.792 | 2803.584 | 2821.571 | 2631.908 | 660 |
There’s a clear relationship between both of the instruments and education, and the coefficients for each are signficiant. The F-statistic for the model is 83, which is higher than 10, which is a good sign of a strong instrument.
We can check for exclusion in part by looking at the relationship between the instruments and the outcome, or wages. We should see some relationship:
ggplot(ed_real_long, aes(x = instrument_value, y = wage)) +
geom_point() +
geom_smooth(method = "lm") +
facet_wrap(~ instrument)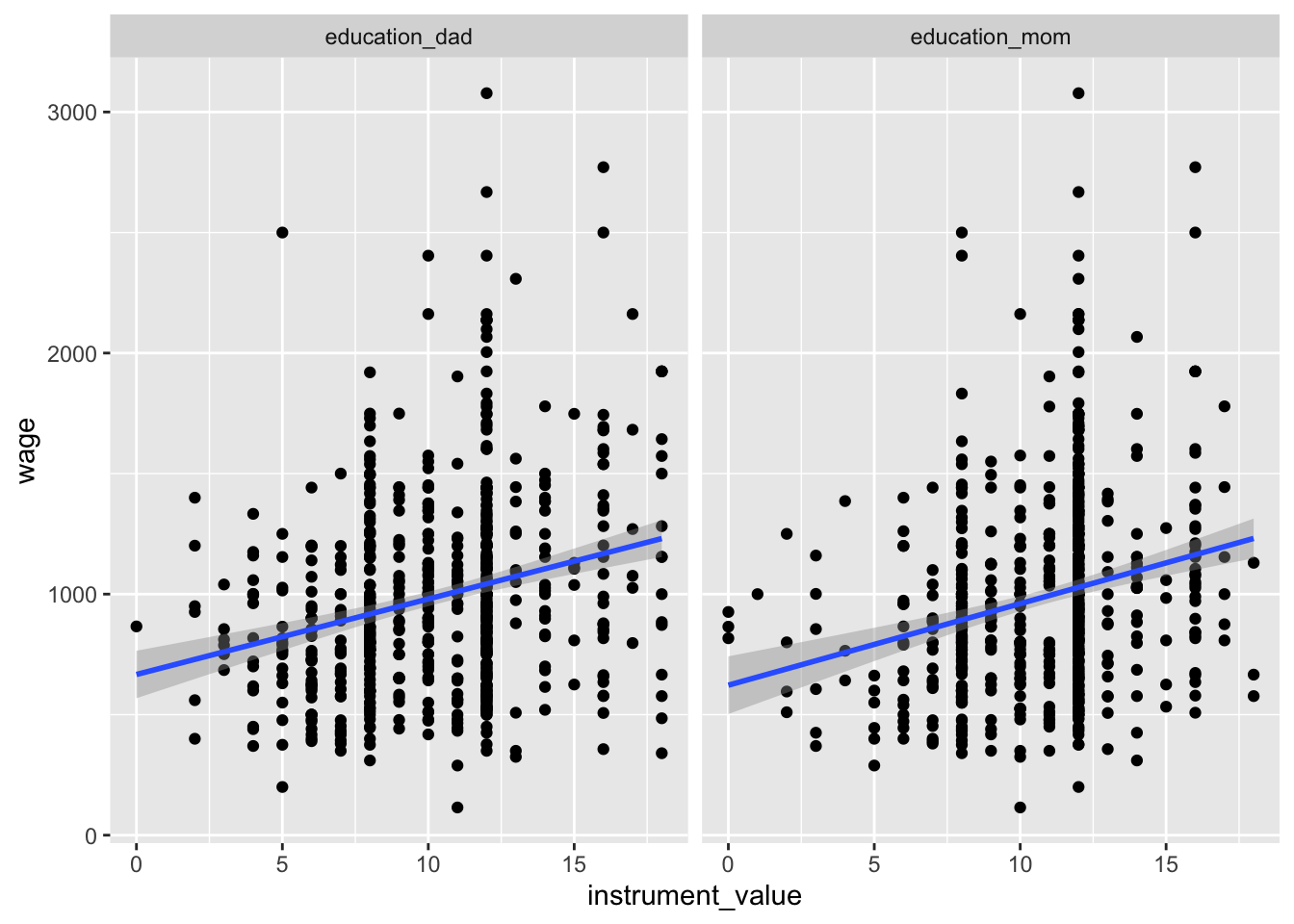
And we do! Now we just have to make the case that the only reason there’s a relationship is that parental education only influences wages through education. Good luck with that.
The last step is to prove exogeneity—that parental education is not correlated with education or wages. Good luck with that too.
Assuming that parental education is a good instrument, we can use it to remove the endogenous part of education using 2SLS. In the first stage, we predict education using our instruments:
We can then extract the predicted education and add it to our main dataset, renaming the .fitted variable to something more useful along the way:
Finally, we can use predicted education to estimate the exogenous effect of education on wages:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -537.7122 | 208.16441 | -2.583113 | 0.010005 |
| education_hat | 111.5614 | 15.17586 | 7.351244 | 0.000000 |
That should arguably be our actual effect! Let’s compare it to the naive model:
| OLS | 2SLS | |
| (Intercept) | 175.160 | -537.712 * |
| (92.839) | (208.164) | |
| education | 59.452 *** | |
| (6.698) | ||
| education_hat | 111.561 *** | |
| (15.176) | ||
| N | 663 | 663 |
| R2 | 0.106 | 0.076 |
| logLik | -4885.974 | -4897.252 |
| AIC | 9777.947 | 9800.503 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | ||
The 2SLS effect is roughly twice as large and is arguably more accurate, since it has removed the endogeneity from education. An extra year of school leads to an extra $111.56 dollars a month in income (in 1980 dollars).
If you don’t want to go through the hassle of doing the two stages by hand, you can use the iv_robust() function from the estimatr package to do both stages at the same time. The second stage goes on the left side of the |, just like a normal regression. The first stage goes on the right side of the |:
model_same_time <- iv_robust(wage ~ education | education_dad + education_mom,
data = ed_real)
tidy(model_same_time)| term | estimate | std.error | statistic | p.value | conf.low | conf.high | df | outcome |
|---|---|---|---|---|---|---|---|---|
| (Intercept) | -537.7122 | 214.43142 | -2.507618 | 0.0123934 | -958.76099 | -116.6633 | 661 | wage |
| education | 111.5614 | 15.90091 | 7.016040 | 0.0000000 | 80.33905 | 142.7838 | 661 | wage |
We should get the same coefficient as the second stage, but the standard errors with iv_robust are more accurate. The only problem with iv_robust is that there’s no way to see the first stage, so if you want to check for relevancy or show the F-test or show the coefficients for the instruments, you’ll have to run a first_stage model on your own.
Models from iv_robust() also work with huxreg(). Note how the education variable isn’t renamed educ_hat in the iv_robust() version—it’s still using predicted education even if it’s not obvious
| OLS | 2SLS | 2SLS automatic | |
| (Intercept) | 175.160 | -537.712 * | -537.712 * |
| (92.839) | (208.164) | (214.431) | |
| education | 59.452 *** | 111.561 *** | |
| (6.698) | (15.901) | ||
| education_hat | 111.561 *** | ||
| (15.176) | |||
| N | 663 | 663 | 663 |
| R2 | 0.106 | 0.076 | 0.025 |
| logLik | -4885.974 | -4897.252 | |
| AIC | 9777.947 | 9800.503 | |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |||
Education, wages, and distance to college (real data)
For this last example we’ll estimate the effect of education on wages using a different instrument—geographic proximity to colleges. This data comes from David Card’s 1995 study where he did the same thing, and it’s available in the wooldridge library as card. You can find a description of all variables here; we’ll use these:
| Variable name | Description |
|---|---|
lwage |
Annual wage (log form) |
educ |
Years of education |
nearc4 |
Living close to college (=1) or far from college (=0) |
smsa |
Living in metropolitan area (=1) or not (=0) |
exper |
Years of experience |
expersq |
Years of experience (squared term) |
black |
Black (=1), not black (=0) |
south |
Living in the south (=1) or not (=0) |
Once again, Card wants to estimate the impact of education on wage. But to solve the ability bias, he utilizes a different instrumental variable: proximity to college. He provides arguments to support each of three main characteristics of a good instrumental variable:
- Relevancy: People who live close to a 4-year college have easier access to education at a lower costs (no commuting costs and time nor accomodation costs), so they have greater incentives to pursue education.
- Exclusion: Proximity to a college has no effect on your annual income, unless you decide to pursue further education because of the nearby college.
- Exogeneity: Individual ability does not depend on proximity to a college.
Therefore, he estimates a model where:
First stage:
\[ \widehat{\text{Educ}} = \beta_0 + \beta_1\text{nearc4} + \beta_{2-6}\text{Control variables} \]
Second stage:
\[ \text{lwage} = \beta_0 + \beta_1 \widehat{\text{Educ}} + \beta_{2-6}\text{Control variables} \]
He controls for five things: smsa66 + exper + expersq + black + south66.
We can do the same thing. IMPORTANT NOTE: When you include controls, every control variable needs to go in both stages. The only things from the first stage that don’t carry over to the second stage are the instruments—notice how nearc4 is only in the first stage, since it’s the instrument, but it’s not in the second stage. The other controls are all in both stages.
# Load data
data("card")
# First we'll build a naive model without any instruments so we can see the bias
# in the educ coefficient
naive_model <- lm(lwage ~ educ + smsa66 + exper + expersq + black + south66,
data = card)
# Then we'll run the first stage, predicting educ with nearc4 + all the controls
first_stage <- lm(educ ~ nearc4 + smsa66 + exper + expersq + black + south66,
data = card)
# Then we'll add the fitted education values into the original dataset and
# rename the .fitted column so it's easier to work with
card <- augment_columns(first_stage, card) %>%
rename(educ_hat = .fitted)
# Finally we can run the second stage model using the predicted education from
# the first stage
second_stage <- lm(lwage ~ educ_hat + smsa66 + exper + expersq + black + south66,
data = card)
# Just for fun, we can do all of this at the same time with iv_robsust
model_2sls <- iv_robust(lwage ~ educ + smsa66 + exper + expersq + black + south66 |
nearc4 + smsa66 + exper + expersq + black + south66,
data = card)| OLS | 2SLS | 2SLS (robust) | |
| (Intercept) | 4.731 *** | 3.357 *** | 3.357 *** |
| (0.069) | (0.926) | (0.930) | |
| educ | 0.076 *** | 0.157 ** | |
| (0.004) | (0.055) | ||
| smsa66 | 0.113 *** | 0.081 ** | 0.081 ** |
| (0.015) | (0.027) | (0.027) | |
| exper | 0.085 *** | 0.118 *** | 0.118 *** |
| (0.007) | (0.023) | (0.024) | |
| expersq | -0.002 *** | -0.002 *** | -0.002 *** |
| (0.000) | (0.000) | (0.000) | |
| black | -0.177 *** | -0.104 | -0.104 * |
| (0.018) | (0.053) | (0.052) | |
| south66 | -0.096 *** | -0.064 * | -0.064 * |
| (0.016) | (0.028) | (0.028) | |
| educ_hat | 0.157 ** | ||
| (0.055) | |||
| N | 3010 | 3010 | 3010 |
| R2 | 0.269 | 0.160 | 0.143 |
| logLik | -1352.703 | -1563.264 | |
| AIC | 2721.406 | 3142.528 | |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |||
Notice how educ_hat and educ are the same in each of the 2SLS models, and they’re higher than the naive uninstrumented model. Because the outcome is log wages, we can say that an extra year of education causes a 15.7% increase in wages.
Clearest and muddiest things
Go to this form and answer these three questions:
- What was the muddiest thing from class today? What are you still wondering about?
- What was the clearest thing from class today?
- What was the most exciting thing you learned?
I’ll compile the questions and send out answers after class.